RESISTÊNCIA DOS MATERIAIS
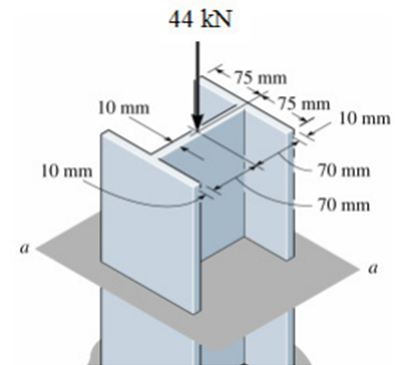
A coluna está submetida a uma força axial de 44 kN no seu topo. Supondo que a seção transversal tenha as dimensões mostradas na figura, determinar a tensão normal média que atua sobre a seção a-a.
10,0 MPa
0,2 MPa
2,0 MPa
0,1 MPa
1,0 MPa
Os dois cabos de aço AB e AC são usados para suportar a carga. Se ambos tiverem uma tensão de tração admissível de 200 MPa, determine o diâmetro exigido para cada cabo se a carga aplicada for P = 5 kN.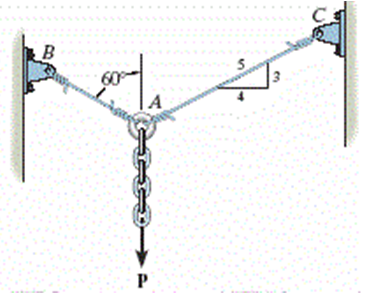
Dab = 10,52 mm ; Dac = 10,96 mm
Dab = 5,26 mm ; Dac = 5,48 mm
Dab = 4,36 mm ; Dac = 4,48 mm
Dab = 15,62 mm ; Dac = 15,84 mm
Dab = 6,26 mm ; Dac = 6,48 mm
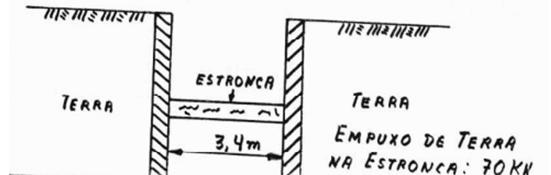
Calcular o diâmetro de uma estronca de madeira, com aproximação a cada 0,5cm, que escora as paredes de contenção provisórias da escavação de terra da figura. A estronca é horizontal e o módulo de elasticidade da madeira é 700KN/cm². A tensão admissível à compressão da madeira é 7 MPa e o fator de segurança de flambagem é 2,5.
D = 12,5 mm
D = 13,5 mm
D = 15,0 mm
D = 11,5 mm
D = 16,0 mm
O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes da tensão que agem no plano inclinado AB.

σx' = 44.82 Mpa; τx'y' = −39.62 Mpa
σx' = 46.99 Mpa; τx'y' = −38.42 Mpa
σx' = −34.82 Mpa; τx'y' = 49.69 Mpa
σx' = 94.69 Mpa; τx'y' = −43.82 Mpa
σx' = 49.69 Mpa; τx'y' = −34.82 Mpa
Qual a máxima carga distribuída q que pode ser aplicada à viga bi-apoiada com 3 metros de comprimento, sabendo-se que €σu = 50 MPa, com um coeficiente de segurança, C.S., para tração = 2,0 e compressão = 1,5 e sendo a sua seção quadrada de lado 20cm.
29,62 KN/M
34,24 KN/M
25,00 KN/M
46,22 KN/M
10,40 KN/M
Um cilindro de aço, de comprimento Lo = 56 mm e diâmetro do = 24 mm, é comprimido entre duas placas rígidas, com uma força P = 45 kN. Se a redução medida no comprimento for de 0,0416 mm, qual é o módulo de elasticidade do material?
118,75 GPa
126,20 GPa
147,32 GPa
133,90 GPa
214,16 GPa
Um corpo de prova com comprimento original de 300 mm tem diâmetro original de 12 mm e é submetido a uma força de 2,5 kN. Quando a força é aumentada para 9 kN, o corpo de prova sofre um alongamento de 22,5 mm. Determine o módulo de elasticidade para o material se ele permanecer elástico.
E = 876,3 MPa
E = 676,3 MPa
E = 766,3 MPa
E = 745,3 MPa
E = 564,3 MPa
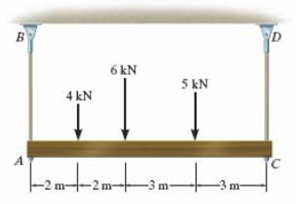
As hastes AB e CD são feitas de aço cuja tensão de ruptura por tração é 510 MPa. Usando um fator de segurança de 1,75 para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em A e C.
dAB = 6.02 mm; dCD = 6.41 mm
dAB = 5,41 mm; dCD = 5.46 mm
dAB = 6.02 mm; dCD = 5.41 mm
dAB = 3.01 mm; dCD = 2.70 mm
dAB = 5.02 mm; dCD = 6.41 mm
Determine a tensão de cisalhamento atuante no ponto B do elemento apresentado na Figura:
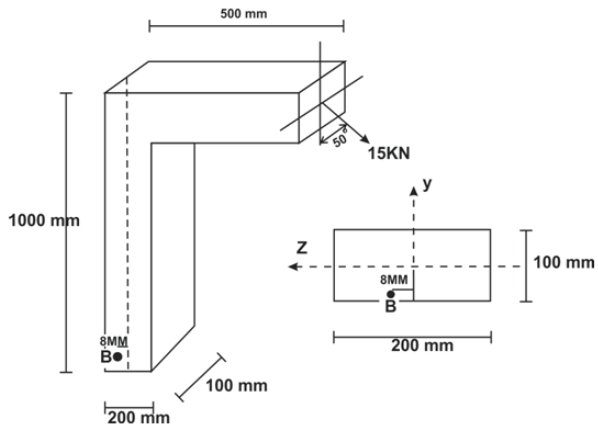
t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa
Um corpo de prova de alumínio tem diâmetro inicial d = 20 mm e comprimento de referência inicial Lo = 240 mm. Quando uma força axial de tração de 120 kN é aplicada, a barra sofre um alongamento de 1,24 mm. Determine a variação no diâmetro. Considere G = 26 GPa.
10,0 MPa
0,2 MPa
2,0 MPa
0,1 MPa
1,0 MPa
Os dois cabos de aço AB e AC são usados para suportar a carga. Se ambos tiverem uma tensão de tração admissível de 200 MPa, determine o diâmetro exigido para cada cabo se a carga aplicada for P = 5 kN.
Dab = 10,52 mm ; Dac = 10,96 mm
Dab = 5,26 mm ; Dac = 5,48 mm
Dab = 4,36 mm ; Dac = 4,48 mm
Dab = 15,62 mm ; Dac = 15,84 mm
Dab = 6,26 mm ; Dac = 6,48 mm
Calcular o diâmetro de uma estronca de madeira, com aproximação a cada 0,5cm, que escora as paredes de contenção provisórias da escavação de terra da figura. A estronca é horizontal e o módulo de elasticidade da madeira é 700KN/cm². A tensão admissível à compressão da madeira é 7 MPa e o fator de segurança de flambagem é 2,5.

D = 12,5 mm
D = 13,5 mm
D = 15,0 mm
D = 11,5 mm
D = 16,0 mm
O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes da tensão que agem no plano inclinado AB.

σx' = 44.82 Mpa; τx'y' = −39.62 Mpa
σx' = 46.99 Mpa; τx'y' = −38.42 Mpa
σx' = −34.82 Mpa; τx'y' = 49.69 Mpa
σx' = 94.69 Mpa; τx'y' = −43.82 Mpa
σx' = 49.69 Mpa; τx'y' = −34.82 Mpa
Qual a máxima carga distribuída q que pode ser aplicada à viga bi-apoiada com 3 metros de comprimento, sabendo-se que €σu = 50 MPa, com um coeficiente de segurança, C.S., para tração = 2,0 e compressão = 1,5 e sendo a sua seção quadrada de lado 20cm.
29,62 KN/M
34,24 KN/M
25,00 KN/M
46,22 KN/M
10,40 KN/M
Um cilindro de aço, de comprimento Lo = 56 mm e diâmetro do = 24 mm, é comprimido entre duas placas rígidas, com uma força P = 45 kN. Se a redução medida no comprimento for de 0,0416 mm, qual é o módulo de elasticidade do material?
118,75 GPa
126,20 GPa
147,32 GPa
133,90 GPa
214,16 GPa
Um corpo de prova com comprimento original de 300 mm tem diâmetro original de 12 mm e é submetido a uma força de 2,5 kN. Quando a força é aumentada para 9 kN, o corpo de prova sofre um alongamento de 22,5 mm. Determine o módulo de elasticidade para o material se ele permanecer elástico.
E = 876,3 MPa
E = 676,3 MPa
E = 766,3 MPa
E = 745,3 MPa
E = 564,3 MPa
As hastes AB e CD são feitas de aço cuja tensão de ruptura por tração é 510 MPa. Usando um fator de segurança de 1,75 para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em A e C.

dAB = 6.02 mm; dCD = 6.41 mm
dAB = 5,41 mm; dCD = 5.46 mm
dAB = 6.02 mm; dCD = 5.41 mm
dAB = 3.01 mm; dCD = 2.70 mm
dAB = 5.02 mm; dCD = 6.41 mm
Determine a tensão de cisalhamento atuante no ponto B do elemento apresentado na Figura:

t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa
Um corpo de prova de alumínio tem diâmetro inicial d = 20 mm e comprimento de referência inicial Lo = 240 mm. Quando uma força axial de tração de 120 kN é aplicada, a barra sofre um alongamento de 1,24 mm. Determine a variação no diâmetro. Considere G = 26 GPa.
Dab = 10,52 mm ; Dac = 10,96 mm
Dab = 5,26 mm ; Dac = 5,48 mm
Dab = 4,36 mm ; Dac = 4,48 mm
Dab = 15,62 mm ; Dac = 15,84 mm
Dab = 6,26 mm ; Dac = 6,48 mm
Calcular o diâmetro de uma estronca de madeira, com aproximação a cada 0,5cm, que escora as paredes de contenção provisórias da escavação de terra da figura. A estronca é horizontal e o módulo de elasticidade da madeira é 700KN/cm². A tensão admissível à compressão da madeira é 7 MPa e o fator de segurança de flambagem é 2,5.

D = 12,5 mm
D = 13,5 mm
D = 15,0 mm
D = 11,5 mm
D = 16,0 mm
O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes da tensão que agem no plano inclinado AB.

σx' = 44.82 Mpa; τx'y' = −39.62 Mpa
σx' = 46.99 Mpa; τx'y' = −38.42 Mpa
σx' = −34.82 Mpa; τx'y' = 49.69 Mpa
σx' = 94.69 Mpa; τx'y' = −43.82 Mpa
σx' = 49.69 Mpa; τx'y' = −34.82 Mpa
Qual a máxima carga distribuída q que pode ser aplicada à viga bi-apoiada com 3 metros de comprimento, sabendo-se que €σu = 50 MPa, com um coeficiente de segurança, C.S., para tração = 2,0 e compressão = 1,5 e sendo a sua seção quadrada de lado 20cm.
29,62 KN/M
34,24 KN/M
25,00 KN/M
46,22 KN/M
10,40 KN/M
Um cilindro de aço, de comprimento Lo = 56 mm e diâmetro do = 24 mm, é comprimido entre duas placas rígidas, com uma força P = 45 kN. Se a redução medida no comprimento for de 0,0416 mm, qual é o módulo de elasticidade do material?
118,75 GPa
126,20 GPa
147,32 GPa
133,90 GPa
214,16 GPa
Um corpo de prova com comprimento original de 300 mm tem diâmetro original de 12 mm e é submetido a uma força de 2,5 kN. Quando a força é aumentada para 9 kN, o corpo de prova sofre um alongamento de 22,5 mm. Determine o módulo de elasticidade para o material se ele permanecer elástico.
E = 876,3 MPa
E = 676,3 MPa
E = 766,3 MPa
E = 745,3 MPa
E = 564,3 MPa
As hastes AB e CD são feitas de aço cuja tensão de ruptura por tração é 510 MPa. Usando um fator de segurança de 1,75 para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em A e C.

dAB = 6.02 mm; dCD = 6.41 mm
dAB = 5,41 mm; dCD = 5.46 mm
dAB = 6.02 mm; dCD = 5.41 mm
dAB = 3.01 mm; dCD = 2.70 mm
dAB = 5.02 mm; dCD = 6.41 mm
Determine a tensão de cisalhamento atuante no ponto B do elemento apresentado na Figura:

t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa
Um corpo de prova de alumínio tem diâmetro inicial d = 20 mm e comprimento de referência inicial Lo = 240 mm. Quando uma força axial de tração de 120 kN é aplicada, a barra sofre um alongamento de 1,24 mm. Determine a variação no diâmetro. Considere G = 26 GPa.
D = 12,5 mm
D = 13,5 mm
D = 15,0 mm
D = 11,5 mm
D = 16,0 mm
O estado de tensão em um ponto em um elemento estrutural é mostrado no elemento. Determine as componentes da tensão que agem no plano inclinado AB.

σx' = 44.82 Mpa; τx'y' = −39.62 Mpa
σx' = 46.99 Mpa; τx'y' = −38.42 Mpa
σx' = −34.82 Mpa; τx'y' = 49.69 Mpa
σx' = 94.69 Mpa; τx'y' = −43.82 Mpa
σx' = 49.69 Mpa; τx'y' = −34.82 Mpa
Qual a máxima carga distribuída q que pode ser aplicada à viga bi-apoiada com 3 metros de comprimento, sabendo-se que €σu = 50 MPa, com um coeficiente de segurança, C.S., para tração = 2,0 e compressão = 1,5 e sendo a sua seção quadrada de lado 20cm.
29,62 KN/M
34,24 KN/M
25,00 KN/M
46,22 KN/M
10,40 KN/M
Um cilindro de aço, de comprimento Lo = 56 mm e diâmetro do = 24 mm, é comprimido entre duas placas rígidas, com uma força P = 45 kN. Se a redução medida no comprimento for de 0,0416 mm, qual é o módulo de elasticidade do material?
118,75 GPa
126,20 GPa
147,32 GPa
133,90 GPa
214,16 GPa
Um corpo de prova com comprimento original de 300 mm tem diâmetro original de 12 mm e é submetido a uma força de 2,5 kN. Quando a força é aumentada para 9 kN, o corpo de prova sofre um alongamento de 22,5 mm. Determine o módulo de elasticidade para o material se ele permanecer elástico.
E = 876,3 MPa
E = 676,3 MPa
E = 766,3 MPa
E = 745,3 MPa
E = 564,3 MPa
As hastes AB e CD são feitas de aço cuja tensão de ruptura por tração é 510 MPa. Usando um fator de segurança de 1,75 para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em A e C.

dAB = 6.02 mm; dCD = 6.41 mm
dAB = 5,41 mm; dCD = 5.46 mm
dAB = 6.02 mm; dCD = 5.41 mm
dAB = 3.01 mm; dCD = 2.70 mm
dAB = 5.02 mm; dCD = 6.41 mm
Determine a tensão de cisalhamento atuante no ponto B do elemento apresentado na Figura:

t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa
Um corpo de prova de alumínio tem diâmetro inicial d = 20 mm e comprimento de referência inicial Lo = 240 mm. Quando uma força axial de tração de 120 kN é aplicada, a barra sofre um alongamento de 1,24 mm. Determine a variação no diâmetro. Considere G = 26 GPa.
σx' = 44.82 Mpa; τx'y' = −39.62 Mpa
σx' = 46.99 Mpa; τx'y' = −38.42 Mpa
σx' = −34.82 Mpa; τx'y' = 49.69 Mpa
σx' = 94.69 Mpa; τx'y' = −43.82 Mpa
σx' = 49.69 Mpa; τx'y' = −34.82 Mpa
Qual a máxima carga distribuída q que pode ser aplicada à viga bi-apoiada com 3 metros de comprimento, sabendo-se que €σu = 50 MPa, com um coeficiente de segurança, C.S., para tração = 2,0 e compressão = 1,5 e sendo a sua seção quadrada de lado 20cm.
29,62 KN/M
34,24 KN/M
25,00 KN/M
46,22 KN/M
10,40 KN/M
Um cilindro de aço, de comprimento Lo = 56 mm e diâmetro do = 24 mm, é comprimido entre duas placas rígidas, com uma força P = 45 kN. Se a redução medida no comprimento for de 0,0416 mm, qual é o módulo de elasticidade do material?
118,75 GPa
126,20 GPa
147,32 GPa
133,90 GPa
214,16 GPa
Um corpo de prova com comprimento original de 300 mm tem diâmetro original de 12 mm e é submetido a uma força de 2,5 kN. Quando a força é aumentada para 9 kN, o corpo de prova sofre um alongamento de 22,5 mm. Determine o módulo de elasticidade para o material se ele permanecer elástico.
E = 876,3 MPa
E = 676,3 MPa
E = 766,3 MPa
E = 745,3 MPa
E = 564,3 MPa
As hastes AB e CD são feitas de aço cuja tensão de ruptura por tração é 510 MPa. Usando um fator de segurança de 1,75 para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em A e C.

dAB = 6.02 mm; dCD = 6.41 mm
dAB = 5,41 mm; dCD = 5.46 mm
dAB = 6.02 mm; dCD = 5.41 mm
dAB = 3.01 mm; dCD = 2.70 mm
dAB = 5.02 mm; dCD = 6.41 mm
Determine a tensão de cisalhamento atuante no ponto B do elemento apresentado na Figura:

t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa
Um corpo de prova de alumínio tem diâmetro inicial d = 20 mm e comprimento de referência inicial Lo = 240 mm. Quando uma força axial de tração de 120 kN é aplicada, a barra sofre um alongamento de 1,24 mm. Determine a variação no diâmetro. Considere G = 26 GPa.
29,62 KN/M
34,24 KN/M
25,00 KN/M
46,22 KN/M
10,40 KN/M
Um cilindro de aço, de comprimento Lo = 56 mm e diâmetro do = 24 mm, é comprimido entre duas placas rígidas, com uma força P = 45 kN. Se a redução medida no comprimento for de 0,0416 mm, qual é o módulo de elasticidade do material?
118,75 GPa
126,20 GPa
147,32 GPa
133,90 GPa
214,16 GPa
Um corpo de prova com comprimento original de 300 mm tem diâmetro original de 12 mm e é submetido a uma força de 2,5 kN. Quando a força é aumentada para 9 kN, o corpo de prova sofre um alongamento de 22,5 mm. Determine o módulo de elasticidade para o material se ele permanecer elástico.
E = 876,3 MPa
E = 676,3 MPa
E = 766,3 MPa
E = 745,3 MPa
E = 564,3 MPa
As hastes AB e CD são feitas de aço cuja tensão de ruptura por tração é 510 MPa. Usando um fator de segurança de 1,75 para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em A e C.

dAB = 6.02 mm; dCD = 6.41 mm
dAB = 5,41 mm; dCD = 5.46 mm
dAB = 6.02 mm; dCD = 5.41 mm
dAB = 3.01 mm; dCD = 2.70 mm
dAB = 5.02 mm; dCD = 6.41 mm
Determine a tensão de cisalhamento atuante no ponto B do elemento apresentado na Figura:

t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa
Um corpo de prova de alumínio tem diâmetro inicial d = 20 mm e comprimento de referência inicial Lo = 240 mm. Quando uma força axial de tração de 120 kN é aplicada, a barra sofre um alongamento de 1,24 mm. Determine a variação no diâmetro. Considere G = 26 GPa.
118,75 GPa
126,20 GPa
147,32 GPa
133,90 GPa
214,16 GPa
Um corpo de prova com comprimento original de 300 mm tem diâmetro original de 12 mm e é submetido a uma força de 2,5 kN. Quando a força é aumentada para 9 kN, o corpo de prova sofre um alongamento de 22,5 mm. Determine o módulo de elasticidade para o material se ele permanecer elástico.
E = 876,3 MPa
E = 676,3 MPa
E = 766,3 MPa
E = 745,3 MPa
E = 564,3 MPa
As hastes AB e CD são feitas de aço cuja tensão de ruptura por tração é 510 MPa. Usando um fator de segurança de 1,75 para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em A e C.

dAB = 6.02 mm; dCD = 6.41 mm
dAB = 5,41 mm; dCD = 5.46 mm
dAB = 6.02 mm; dCD = 5.41 mm
dAB = 3.01 mm; dCD = 2.70 mm
dAB = 5.02 mm; dCD = 6.41 mm
Determine a tensão de cisalhamento atuante no ponto B do elemento apresentado na Figura:

t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa
Um corpo de prova de alumínio tem diâmetro inicial d = 20 mm e comprimento de referência inicial Lo = 240 mm. Quando uma força axial de tração de 120 kN é aplicada, a barra sofre um alongamento de 1,24 mm. Determine a variação no diâmetro. Considere G = 26 GPa.
E = 876,3 MPa
E = 676,3 MPa
E = 766,3 MPa
E = 745,3 MPa
E = 564,3 MPa
As hastes AB e CD são feitas de aço cuja tensão de ruptura por tração é 510 MPa. Usando um fator de segurança de 1,75 para tração, determine o menor diâmetro das hastes de modo que elas possam suportar a carga mostrada. Considere que a viga está acoplada por pinos em A e C.

dAB = 6.02 mm; dCD = 6.41 mm
dAB = 5,41 mm; dCD = 5.46 mm
dAB = 6.02 mm; dCD = 5.41 mm
dAB = 3.01 mm; dCD = 2.70 mm
dAB = 5.02 mm; dCD = 6.41 mm
Determine a tensão de cisalhamento atuante no ponto B do elemento apresentado na Figura:

t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa
Um corpo de prova de alumínio tem diâmetro inicial d = 20 mm e comprimento de referência inicial Lo = 240 mm. Quando uma força axial de tração de 120 kN é aplicada, a barra sofre um alongamento de 1,24 mm. Determine a variação no diâmetro. Considere G = 26 GPa.

dAB = 6.02 mm; dCD = 6.41 mm
dAB = 5,41 mm; dCD = 5.46 mm
dAB = 6.02 mm; dCD = 5.41 mm
dAB = 3.01 mm; dCD = 2.70 mm
dAB = 5.02 mm; dCD = 6.41 mm
Determine a tensão de cisalhamento atuante no ponto B do elemento apresentado na Figura:

t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa
Um corpo de prova de alumínio tem diâmetro inicial d = 20 mm e comprimento de referência inicial Lo = 240 mm. Quando uma força axial de tração de 120 kN é aplicada, a barra sofre um alongamento de 1,24 mm. Determine a variação no diâmetro. Considere G = 26 GPa.

t = 0,68 MPa
t = 0,86 MPa
t = 1,96 MPa
t = 0,48 MPa
t = 1,48 MPa